Building a Pathfinding Visualizer in Rust

I recently built a pathfinding visualizer in Rust as a way to better understand how different graph traversal algorithms work. There’s something satisfying about watching an algorithm explore a maze in real-time, seeing the frontier expand as it searches for the optimal path.

You can try it yourself at joonaspessi.github.io/path_finding.

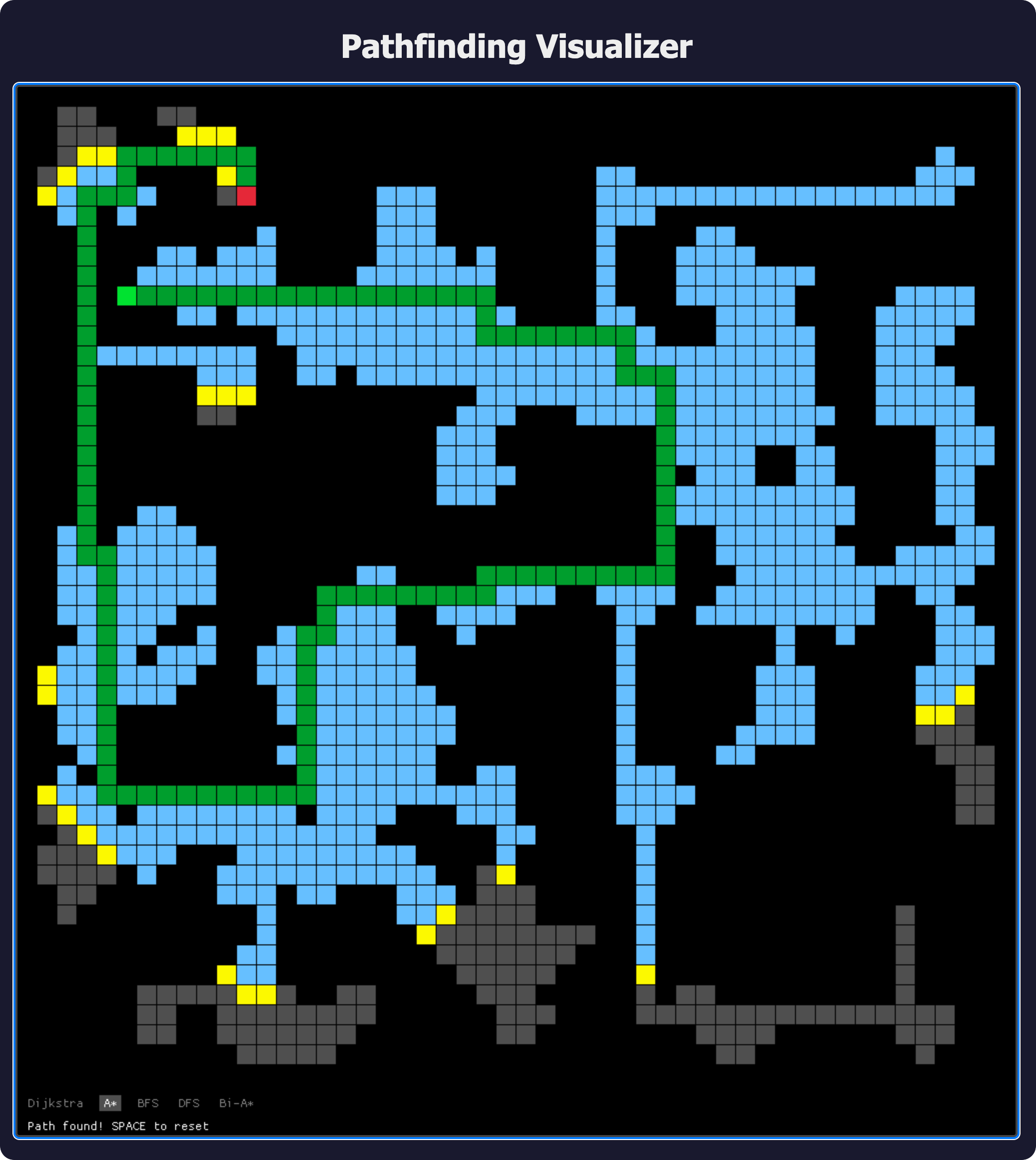
The Algorithms

The visualizer implements five different pathfinding algorithms, each with its own exploration strategy:

• Dijkstra’s Algorithm explores outward uniformly, guaranteeing the shortest path but visiting many unnecessary nodes
• A* adds a heuristic to guide the search toward the goal, making it much more efficient
• Bidirectional A* runs two searches simultaneously from both ends, meeting in the middle
• Breadth-First Search explores level by level, simple but effective for unweighted grids
• Depth-First Search dives deep before backtracking, often finding suboptimal paths

Implementation

Source code for the implementation can be found from github joonaspessi/path_finding

All algorithms implement a common trait that standardizes how they execute:

pub trait PathfindingAlgorithm {
    fn step(&mut self, grid: &Grid) -> bool;
    fn is_finished(&self) -> bool;
    fn get_path(&self) -> Option<Vec<(usize, usize)>>;
    fn get_visited(&self) -> &HashSet<(usize, usize)>;
    fn get_queue(&self) -> Vec<(usize, usize)>;
}

This design makes it trivial to swap between algorithms at runtime. Each algorithm maintains its own state and advances one step at a time, allowing the visualizer to render the exploration process.

Procedural Cave Generation

To make the visualizer more interesting, I added a cellular automata-based cave generator. The process works in four phases:

1. Randomly fill the grid with walls at 45% probability
2. Apply smoothing passes to create natural-looking cave structures
3. Connect isolated regions with corridors using flood-fill detection
4. Place start and end points at the furthest reachable positions

The smoothing step uses a simple rule: if a cell has more than 4 wall neighbors, it becomes a wall; otherwise it becomes empty. After a few iterations, this produces organic-looking cave systems.

Technical Stack

The project is built with macroquad, a simple Rust game library that compiles to both native and WebAssembly. This made it easy to deploy to GitHub Pages while keeping the development experience straightforward.

The controls are simple: left-click to toggle walls, right-click to place start and end points, Tab to switch algorithms, and Space to run the pathfinding. Press G to generate a new random cave.

Building this visualizer was a great way to internalize how these algorithms actually behave, beyond just reading about their time complexity. Seeing A* laser-focus toward the goal while Dijkstra methodically explores everything makes the theoretical advantages tangible.